先日あげた、構造的把握力検査の問題形式2つのうちの1つ「算数の計算問題の構造をつかむ」問題について、解答・解説していきます。

問題はコチラ。

解答　B

解説

まず、与えられている条件のタイプを考えてみよう。隠された条件にも注意が必要である。

ア　昼と夜の時間差が与えられているが、1日は24時間 (これが隠された条件) なのだから、2つの量の和と差が与えられていることに他ならない。

イ　年齢の差と割合が与えられている。

ウ　所持金の和と差が与えられているので、アと同じ計算構造になることがわかる。

エ　イと似ていると思うかもしれないが、年齢の比と和なので、異なる計算になる。

参考

それぞれの文章題の答えを求める必要はないが、参考のために次に示しておこう。

アとウは連立方程式でも解けるが、（アの場合）2つの量a（長い昼の時間）とb（短い昼の時間）について、和a＋bと差a－bが与えられているとき、次のようにしてa、bが簡単に求められることは覚えておいて損がない。この解法を「和差算」といい、私立中学入試の算数問題ではよく使われる計算法である。

a＝(和＋差)÷2
b＝(和－差)÷2

アを図で説明すると

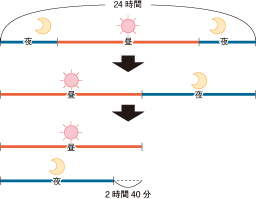
すると、アは

(24＋8/3)÷2＝40/3=13 1/3 (時間）

すなわち 13時間20分

ウを図で説明すると

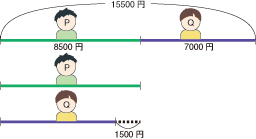
ウは

(15500＋1500)÷2＝8500 (円)

イを図で説明すると

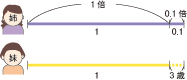
またイは、年齢差が1.1－1＝0.1の割合にあたるから

3÷0.1＝30 (歳)

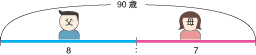
エを図で説明すると

エは、比例配分の計算をして

90×(8－7)/(8＋7)＝90×1/5＝6 (歳)

となる。

いかがだったでしょうか。
次回は、もう1つの問題形式「グルーピング」について考えていきます。

追記2014/03/13

本をお探しの方は上記をご参照ください。